Continuando con los ejercicios de programación, hoy veremos uno muy interesante, donde vamos a calcular Pi con Python, pero antes que nada ¿Qué es el número Pi?
El número Pi es la relación entre la longitud de una circunferencia y su diámetro en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:
π = 3.141 592 653 589 793 238 462 …
El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e.
Ahora que sabemos un poco sobre Pi, vamos a calcularlo con la serie de Leibniz, la cual no es una de las mejores formulas para obtener el valor de Pi, ya que se requieren demasiadas iteraciones para obtener los primeros decimales de Pi. Para calcular π con 10 decimales correctos hacen falta más de cinco mil millones de operaciones matemáticas. Pero que para este ejercicio de ciclos, nos viene bien para probarlo.
Serie de Leibniz
La serie de Leibniz será nuestro modelo matemático con el cual calcularemos el valor de Pi, la serie es:
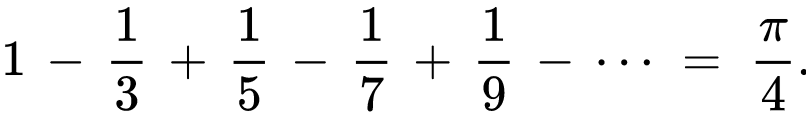
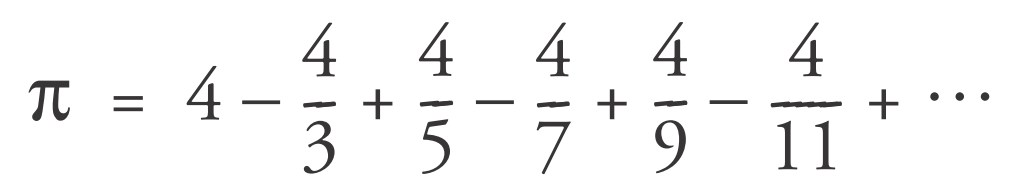
Código
Para poder calcular Pi con la serie de Leibniz debemos saber cuantas iteraciones o términos de la serie queremos usar, entonces lo primero es leer el número de términos de la serie, lo multiplicamos por 2 y lo guardamos en una variable. Se multiplica por dos porque la serie no utiliza los términos con denominador par, entonces de por ejemplo si pedimos 50 términos, en realidad usaría 25. Después inicializamos con 0 la variable donde guardaremos el valor de Pi.
Ahora que tenemos el número de términos que usaremos de la serie, creamos un ciclo que inicia en 1 y termina en el número total de términos, pero especificamos que cada ciclo avance dos posiciones, esto debido a que los denominadores de la serie son números impares, y si comenzamos con 1, para llegar al 3 avanzamos 2 posiciones en el rango, y lo mismo para los siguientes términos. Con eso vamos a iterar en cada uno de los elementos de la serie.
Ya dentro del ciclo, y analizando la serie vemos que el primer término es positivo, el segundo negativo y así consecutivamente, los términos van cambiando de signo conforme avanza la serie. Para esto podemos tener una variable contadora, que lleve el número de términos, y de acuerdo a si es par o impar, cambiará el signo del termino dentro de la ecuación. Por lo cual inicializamos a 1 el contador, y de ahí con cada término, el contador se incrementa en 1, además verificamos si es par o impar y en consecuencia sumamos o restamos ese término de la serie.
Podemos poner en cada iteración de la serie que imprima la fracción y su signo, para tener una idea de como va el cálculo. Como resultado tenemos esta primera versión del código:
# Leemos el número de términos
term = 2 * (int(input('Introduzca cuantos terminos de la serie quiere calcular para π: ')))
# Iniciamos la variable que guardará el valor de Pi y el contador de términos de la serie
pi = 0
contador = 1
# Iteramos todos los términos de la serie, comenzando en 1, hasta el número de términos
# y avanzando 2 posiciones cada vez, debido a que la serie no necesita los denominadores pares.
# También debemos recordar que en la función range() se detiene uno antes del numero superior,
# por eso se le suma 1 al número de términos a analizar
for t in range(1,term+1,2):
# Checamos si el contador es par o no para determinar si se suma o se resta el término actual
if contador % 2 :
# Si es par se suma
pi += 4/t
# Se imprime el elemento de la serie y el valor actual de Pi
print(f'Termino número {contador} -> + 4 / {t} Valor de π: {pi:>.20f}')
else:
# Si es impar se resta
pi -= 4/t
# Se imprime el elemento de la serie y el valor actual de Pi
print(f'Termino número {contador} -> - 4 / {t} Valor de π: {pi:>.20f}')
# Se incrementa el contador para el siguiente ciclo
contador +=1 Y al probarlo vemos que funciona bien, realiza todas las operaciones, pero como se menciono al principio, la serie de Leibniz requiere demasiadas iteraciones para comenzar a tener los primeros decimales de Pi correctos, por ejemplo:
Introduzca cuantos terminos de la serie quiere calcular para π: 50
Termino número 1 -> + 4 / 1 Valor de π: 4.00000000000000000000
Termino número 2 -> - 4 / 3 Valor de π: 2.66666666666666696273
Termino número 3 -> + 4 / 5 Valor de π: 3.46666666666666678509
Termino número 4 -> - 4 / 7 Valor de π: 2.89523809523809561028
Termino número 5 -> + 4 / 9 Valor de π: 3.33968253968254025210
Termino número 6 -> - 4 / 11 Valor de π: 2.97604617604617649462
Termino número 7 -> + 4 / 13 Valor de π: 3.28373848373848442606
Termino número 8 -> - 4 / 15 Valor de π: 3.01707181707181781860
Termino número 9 -> + 4 / 17 Valor de π: 3.25236593471887669438
Termino número 10 -> - 4 / 19 Valor de π: 3.04183961892940324390
Termino número 11 -> + 4 / 21 Valor de π: 3.23231580940559393156
Termino número 12 -> - 4 / 23 Valor de π: 3.05840276592733317784
Termino número 13 -> + 4 / 25 Valor de π: 3.21840276592733331995
Termino número 14 -> - 4 / 27 Valor de π: 3.07025461777918540207
Termino número 15 -> + 4 / 29 Valor de π: 3.20818565226194385431
Termino número 16 -> - 4 / 31 Valor de π: 3.07915339419742783988
Termino número 17 -> + 4 / 33 Valor de π: 3.20036551540954894435
Termino número 18 -> - 4 / 35 Valor de π: 3.08607980112383462057
Termino número 19 -> + 4 / 37 Valor de π: 3.19418790923194251263
Termino número 20 -> - 4 / 39 Valor de π: 3.09162380666783986882
Termino número 21 -> + 4 / 41 Valor de π: 3.18918478227759605304
Termino número 22 -> - 4 / 43 Valor de π: 3.09616152646364239942
Termino número 23 -> + 4 / 45 Valor de π: 3.18505041535253141660
Termino número 24 -> - 4 / 47 Valor de π: 3.09994403237380788951
Termino número 25 -> + 4 / 49 Valor de π: 3.18157668543503246994
Termino número 26 -> - 4 / 51 Valor de π: 3.10314531288601269665
Termino número 27 -> + 4 / 53 Valor de π: 3.17861701099922022706
Termino número 28 -> - 4 / 55 Valor de π: 3.10588973827194747557
Termino número 29 -> + 4 / 57 Valor de π: 3.17606517686843847770
Termino número 30 -> - 4 / 59 Valor de π: 3.10826856669894713292
Termino número 31 -> + 4 / 61 Valor de π: 3.17384233719075048441
Termino número 32 -> - 4 / 63 Valor de π: 3.11035027369868721792
Termino número 33 -> + 4 / 65 Valor de π: 3.17188873523714853775
Termino número 34 -> - 4 / 67 Valor de π: 3.11218724269983493258
Termino número 35 -> + 4 / 69 Valor de π: 3.17015825719258836912
Termino número 36 -> - 4 / 71 Valor de π: 3.11382022902357435967
Termino número 37 -> + 4 / 73 Valor de π: 3.16861474957151934007
Termino número 38 -> - 4 / 75 Valor de π: 3.11528141623818610739
Termino número 39 -> + 4 / 77 Valor de π: 3.16722946818623807275
Termino número 40 -> - 4 / 79 Valor de π: 3.11659655679383318372
Termino número 41 -> + 4 / 81 Valor de π: 3.16597927284321567498
Termino número 42 -> - 4 / 83 Valor de π: 3.11778650175887817042
Termino número 43 -> + 4 / 85 Valor de π: 3.16484532528828976794
Termino número 44 -> - 4 / 87 Valor de π: 3.11886831379403695053
Termino número 45 -> + 4 / 89 Valor de π: 3.16381213401875616142
Termino número 46 -> - 4 / 91 Valor de π: 3.11985609006271236154
Termino número 47 -> + 4 / 93 Valor de π: 3.16286684275088436635
Termino número 48 -> - 4 / 95 Valor de π: 3.12076157959298949862
Termino número 49 -> + 4 / 97 Valor de π: 3.16199869299505120779
Termino número 50 -> - 4 / 99 Valor de π: 3.12159465259101098766Vemos que con los primeros 50 términos, el valor de pi apenas comienza a mostrarse, siendo 3.1 el valor más cercano al real. Entonces para tener valores más cercanos al redondeado y clásico 3.1416 debemos calcular más términos, pero ¿cuántos serán necesarios para estar cerca de ese 3.1416?
Vamos a probar con más términos, digamos 500, solo que mostraremos los últimos términos y valores para resumir:
...
Termino número 480 -> - 4 / 959 Valor de π: 3.13950932251701031461
Termino número 481 -> + 4 / 961 Valor de π: 3.14367165342231746905
Termino número 482 -> - 4 / 963 Valor de π: 3.13951796702564056574
Termino número 483 -> + 4 / 965 Valor de π: 3.14366304474584801198
Termino número 484 -> - 4 / 967 Valor de π: 3.13952654009228027121
Termino número 485 -> + 4 / 969 Valor de π: 3.14365450706854465679
Termino número 486 -> - 4 / 971 Valor de π: 3.13953504259892568484
Termino número 487 -> + 4 / 973 Valor de π: 3.14364603951567778140
Termino número 488 -> - 4 / 975 Valor de π: 3.13954347541311351577
Termino número 489 -> + 4 / 977 Valor de π: 3.14363764122682898261
Termino número 490 -> - 4 / 979 Valor de π: 3.13955183938821802414
Termino número 491 -> + 4 / 981 Valor de π: 3.14362931135559842133
Termino número 492 -> - 4 / 983 Valor de π: 3.13956013536373657047
Termino número 493 -> + 4 / 985 Valor de π: 3.14362104906932016135
Termino número 494 -> - 4 / 987 Valor de π: 3.13956836416557161229
Termino número 495 -> + 4 / 989 Valor de π: 3.14361285354878683407
Termino número 496 -> - 4 / 991 Valor de π: 3.13957652660630470720
Termino número 497 -> + 4 / 993 Valor de π: 3.14360472398797652360
Termino número 498 -> - 4 / 995 Valor de π: 3.13958462348546385456
Termino número 499 -> + 4 / 997 Valor de π: 3.14359665959378897782
Termino número 500 -> - 4 / 999 Valor de π: 3.13959265558978506405Vemos que con 500 elementos de la serie, los dígitos comienzan a oscilar entre 3.13 y 3.14, lo cual nos indica que necesitamos más, pero mucho más para poder acercarnos al valor de 3.1416 que queremos.
Para no alargar esto y que se den una idea de cuantas iteraciones se necesitan, el valor de Pi cercano a 3.1416 aparece en el término 9317 de la serie:
...
Termino número 9310 -> - 4 / 18619 Valor de π: 3.14148524220448566169
Termino número 9311 -> + 4 / 18621 Valor de π: 3.14170005343911329376
Termino número 9312 -> - 4 / 18623 Valor de π: 3.14148526527394134078
Termino número 9313 -> + 4 / 18625 Valor de π: 3.14170003037461231798
Termino número 9314 -> - 4 / 18627 Valor de π: 3.14148528833348938960
Termino número 9315 -> + 4 / 18629 Valor de π: 3.14170000732001586385
Termino número 9316 -> - 4 / 18631 Valor de π: 3.14148531138313646949
# Primera aparición de 3.1416....
Termino número 9317 -> + 4 / 18633 Valor de π: 3.14169998427531682594
Termino número 9318 -> - 4 / 18635 Valor de π: 3.14148533442288879769
Termino número 9319 -> + 4 / 18637 Valor de π: 3.14169996124050987518
Termino número 9320 -> - 4 / 18639 Valor de π: 3.14148535745275303555
Termino número 9321 -> + 4 / 18641 Valor de π: 3.14169993821558746205Y conforme se necesiten más dígitos correctos, se debe incrementar el número de términos a analizar, como ejemplo, para los siguientes dígitos que serían 3.14159, se necesitan más de 150,000 elementos. Es por esto que la serie de Leibniz no es la más adecuada para calcular Pi, pero nos sirvió para probar los ciclos for en python.
Cabe mencionar que este código nos da un resultado descriptivo, pero entre mayor sea el número de elementos a calcular, tardará más en procesar el resultado final de nuestro Pi. Es por ello, que en vez de imprimir el resultado en cada iteración podemos imprimirlo sólo cuando sea múltiplo de 100 o de 1000, o del valor que creamos necesario, en el siguiente código muestro la modificación para mostrar el resultado solo cada 100 iteraciones:
# Leemos el número de términos
term = 2*(int(input('Introduzca cuantos terminos de la serie quiere calcular para π: ')))
# Iniciamos la variable que guardará el valor de Pi y el contador de términos de la serie
pi = 0
contador = 1
# Iteramos todos los términos de la serie, comenzando en 1, hasta el número de términos
# y avanzando 2 posiciones cada vez, debido a que la serie no necesita los denominadores pares.
# También debemos recordar que en la función range() se detiene uno antes del numero superior,
# por eso se le suma 1 al número de términos a analizar
for t in range(1,term+1,2):
# Checamos si el contador es par o no para determinar si se suma o se resta el término actual
if contador % 2 :
# Si es par se suma
pi += 4/t
else:
# Si es impar se resta
pi -= 4/t
# Imprimimos el resultado cada 100 iteraciones
if contador%100 == 0 :
print(f'Termino número {contador} -> Valor de π: {pi:>.20f}')
# Se incrementa el contador para el siguiente ciclo
contador +=1
print(f'Para los {contador-1} elementos de la serie, el valor de π es: {pi:>.20f}')Y probamos de nuevo para un número elevado de elementos de la serie, como por ejemplo 10,000:
Introduzca cuantos terminos de la serie quiere calcular para π: 10000
Termino número 100 -> Valor de π: 3.13159290355855368659
Termino número 200 -> Valor de π: 3.13659268483881614742
Termino número 300 -> Valor de π: 3.13825932951559138928
Termino número 400 -> Valor de π: 3.13909265749601429363
Termino número 500 -> Valor de π: 3.13959265558978506405
# Para resumir el resultado no mostramos el segmento del 600 al 9400
Termino número 9500 -> Valor de π: 3.14148739043218139244
Termino número 9600 -> Valor de π: 3.14148848692340187938
Termino número 9700 -> Valor de π: 3.14148956080655272771
Termino número 9800 -> Valor de π: 3.14149061277372387835
Termino número 9900 -> Valor de π: 3.14149164348903209287
Termino número 10000 -> Valor de π: 3.14149265359003448950
Para los 10000 elementos de la serie, el valor de π es: 3.14149265359003448950Y ya en la ejecución es mucho más rápido comparado con el primer ejemplo, y podemos ir analizando como converge el resultado de Pi a los valores conocidos.
Espero les sirva este ejercicio de programación, ustedes pueden hacer su propia versión, optimizar estos ejemplos, lo que deseen. Nos vemos en el próximo ejercicio.





